本文来自微信公众号:孤独大脑(ID:lonelybrain),作者:老喻,原文标题:《永不沉没》,题图来源:《泰坦尼克号》剧照
一
号称永不沉没的泰坦尼克号,为什么第一次航行就沉了?
在电影《泰坦尼克》中,总设计师解释了该船重要的安全保障之一:水密隔舱。
如下图,泰坦尼克号有16个单独的水密隔舱,舱与舱之间的水密门用电动开关控制,即使有4个隔舱同时进水,也会安然无恙。

比泰坦尼克号更早一千年,唐代的泉州已经掌握了“水密隔舱”技术。
《马可·波罗游记》描述的中国南方海船的船壳是多层板结构,还有水密隔舱十三个:“若干最大船舶有内舱到十三所,互以厚板隔之,其用在防海险,如船体触礁或触饿鲸而海水渗入之事。”

采用“水密隔舱”技术的宋代沉船
既然如此,为什么泰坦尼克号会一撞即沉呢?
二
与上述“水密隔舱”技术相关的主要原因是:泰坦尼克号的水密隔舱并不是封顶的。

如上图,当海水漫进第几个隔仓之后,假如导致船体出现较大倾斜,水会蔓延到下一个隔舱,如多米诺骨牌般引起连锁反应,直至更大倾斜、解体、沉没。
这个设计缺陷,恰是对“水密隔舱”技术的数学原理的破坏。
“水密隔舱”技术,是利用了概率上的独立性。
关于“随机事件的独立性”,书中对其的解释是:

举例说:你将一枚标准硬币扔两次,每次都朝上的概率是多少?
假如第一次扔硬币是随机事件A,第二次扔硬币是随机事件B,因为两次的结果互不影响,可以认为是独立的,所以两次都朝上的概率是:1/2×1/2=1/4。
回到泰坦尼克号,我们将模型简化一下:
这是一艘很大的船,假设一次意外事件只破坏一个独立的隔舱;
假设发生意外事件的概率是5%。
那么连续发生四次“独立的、导致破坏一个隔舱的意外事件”的概率是多少呢?
计算如下:
5%×5%×5%×5%=0.000625%,也就是约为百万分之六的概率。
简单来说,这个概率要小于“一个人在一年中被雷劈”的概率。所以,宣传“泰坦尼克号永不沉没”,并非吹牛。
问题在于:
泰坦尼克号的“水密隔舱”技术,并没有让每个隔舱漏水成为“独立事件”;
冰山一下子破坏了5个隔舱。
一个牢不可破的神话,被意外的黑天鹅事件击破了。
三
随机性“支配”着这个世界。
泰坦尼克号偶然遇见了一座冰山。
船员提前用肉眼看见了“两个东西”。因为船上的超远距离望远镜居然被锁住了,所以等亲眼望见时,已经离冰山很近。
分不清这是黑天鹅,还是灰犀牛。
值班的大副作为决策者,给出了两个指示:左满舵,全速倒车。这是一个专业并且本能的反应。
然而,据说舵手执行错误,向右转了——这还不是关键。
更糟的是,大副试图避开冰山的判断根本就是错的。
假如只是减速,让最坚固的船头撞上冰山,水密隔舱的设计可能会发挥作用,泰坦尼克号也许不会沉没。
选择转向,将脆弱的船腰暴露给了冰山,船身被划开一个93米长的大口子,一连损坏了5个水密隔舱。
本来是概率极低的5个独立事件,突然变得不独立了。
概率不再保护这艘原本只有百万分之一可能性沉没的巨轮,2小时40分钟后,泰坦尼克号百分之百地没入冰海。
四
利用“随机事件的独立性”,来实现概率上的“保护系统”,是非常高明的做法。
例如,狡兔三窟。假如一个兔子洞的安全程度是80%,兔子想要更安全,有两种做法:
1. 努力将兔子洞的安全程度提高至95%;
2. 有三个安全程度都是80%的兔子洞。
第一种做法,可能后面为了提升几个百分点,成本会非常高,而且容易有瓶颈;
第二种做法,三个兔子洞都被捣毁的概率是:0.2×0.2×0.2=0.008,所以兔子的安全程度达到了:100%-0.8%=99.2%。
传统载人飞船搭载的星载计算机和控制器,为了实现高性能和高可靠性,要使用昂贵的宇航级器件,整套成本高达约1.4亿人民币。
而SpaceX的龙飞船主控系统的芯片组,却只用了2.6万人民币。
“他们使用了Intel的X86双核处理器,将双核拆成了两个单核,分别计算同样的数据。每个系统配置3块芯片做冗余,也就是6个核做计算。”

对比起机械时代的“水密隔舱”,多个相对独立的芯片不仅构成冗余,又通过数据同步和系统纠错整合在一起。
“如果其中1个核的数据和其他5个核不同,那么主控系统会告诉这个核重新启动,再把其他5个核的数据拷贝给重启的核,从而达到数据一直同步。周而复始,不让一个核掉队。”(参见下图)
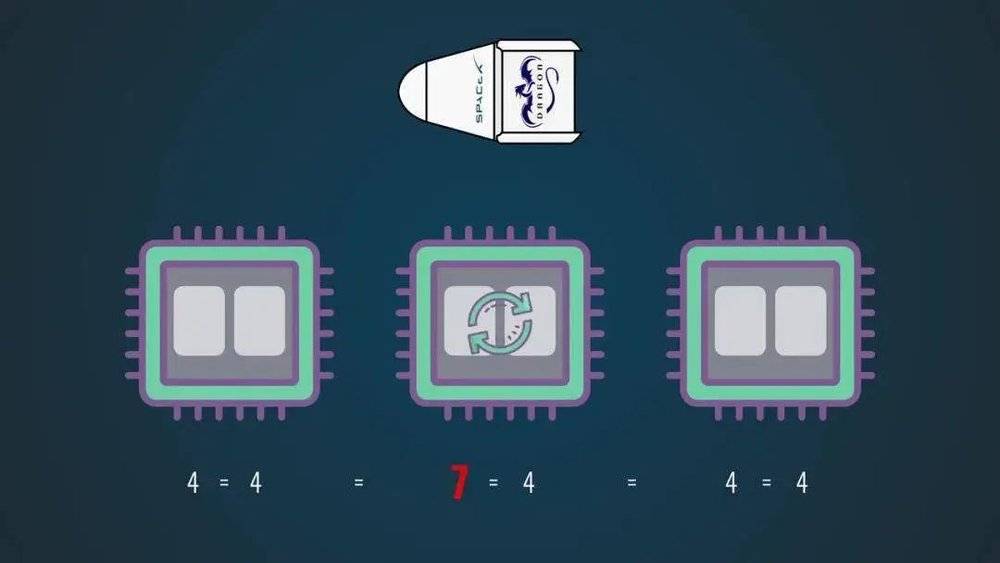
以上案例的文字和图片来自“九天微星”
不是不让意外发生,也不是只增加冗余,还能通过适应性纠错,实现系统的主动安全。
不仅计算机系统可以如此,连火箭的发动机系统也不例外。
“猎鹰”系列火箭梅林发动机应用“简单即可靠”的新理念,将结构设计得非常简单,以消除复杂结构带来的不稳定隐患。
“猎鹰”9号,将九个梅林发动机并联在一起,实现了“简单、可靠、低成本”。
光简单还不行,梅林发动机具备推力补偿技术,能在大范围内调整推力。
2012年10月,“猎鹰”火箭发射“龙”飞船向国际空间运送货物时,第一级的一台发动机出现故障停机,其他8台发动机立即自动补偿了推力损失,最终成功将“龙”飞船送入预定轨道。(上述案例来自网络)
对比起单独追求单一系统或者硬件的牢靠性,通过多系统和多硬件来构成冗余,不仅成本低,出错概率小,还能够主动纠错,有更强的健壮性和适应力。
“不确定性”犹如流水,很难用硬堵的方式去消除。《谁在掷骰子》一书写道:
“泰坦尼克号”沉没后,船只被要求配备更多的救生艇。然而,救生艇的自重导致了“伊斯特兰号”邮轮在密歇根湖倾覆,一共有八百多人遇难。
作者如是总结:意外后果定律可以挫败最良好的意愿。
我们无法用古代加高加厚城墙的方式来堆砌出“确定性”。毕竟,无处不在的墨菲定律“决定”了:“会出错的,终将出错”。
五
让我们回到“随机事件的独立性”。
一个标准硬币随机扔了二十次都是正面朝上,下一次再扔正面朝上的概率还是50%。
因为每次扔硬币(假如没作弊的话)都是独立事件,与之前独立事件的结果无关。
我曾经在赌场观察过押大小赌桌旁的人群,发现大致分为两种:
1. 新赌徒喜欢跟着趋势下注,例如某个桌面连续出了很多个大,那么他们会继续押大。他们在现实生活中可能也会相信“手气、势头、运势、类K线图”等等;
2. 老赌徒喜欢在连续出了很多个大之后,去押小。他们相信“回归”和“反转”。
上述老赌徒的做法,被称为赌徒谬误:
该错误信念,以为随机序列中一个事件发生的机会率与之前发生的事件有关,即其发生的机会率会随着之前没有发生该事件的而上升。
然而,对赌徒谬误的描述,大多时候冤枉了老赌徒们。事实上他们理解独立事件,也没有觉得每一次扔骰子之间有直接相关的联系。
老赌徒相信的是大数定律:扔硬币正面朝上的概率是50%,现在已经连续十次朝上了,根据大数定律,难道不该“回归”到更有机会出现朝下吗?
事实上,大数定律并不会有一双无形的手,将没有遵循其“正确结果”的概率拉回到“正确”的数值上。
没错,依照大数定律,一枚标准硬币一直随机扔很多次,概率会“回到”50%。
但这并非是因为有什么内在的力量在起作用,而是大量重复的随机性用更多50%稀释了那“连续十次”朝上的不均匀结果。
我偏向于用“小数法则”(该法则其实是谬误)来替代“赌徒谬误”的提法。因为老赌徒的思维偏差,是误认为大数法则也适用于小样本。他们忽视了样本大小的影响,觉得小样本和大样本具有同样的期望值。
例如有个家伙在玩儿狼人杀的时候,“聪明”地认为一个人只有很小概率连续三次是杀手,他是在试图运用大数定律。
但是,小样本无法“唤醒”大数定律。
“重复很多次”,是个很有趣的概念:
人们通过重复让小概率的事情发生(有点儿像蛮力版的“遍历性”);
通过重复优化概率(例如精益创业这类贝叶斯更新的实践);
通过重复让大数定律“显灵”。
无论是看得见的东西,还是看不见的概率,人类在思考问题时不可避免地会陷入因果论和目的论。
例如,尽管学了很多年牛顿力学,我们的直觉还会觉得亚里士多德的古老观点是对的:力是维持物体运动状态的原因。
同样,我们觉得随机性会像上帝之手般去主动调节出现了偏差的概率。
认为这个世界“有目的”,觉得万事万物之间是被因果关系联系起来的,这是人类根深蒂固的错觉。
所以,我喜欢休谟、斯密、达尔文和玻尔兹曼:
休谟斩断了我们由来已久的对因果的幻觉和迷恋;
斯密和达尔文则将随机性与人类社会以及生命之谜关联起来;
而玻尔兹曼则用概率来解释物理学。
按照他们的哲学,一件事情发生了,是因为这件事情的发生概率比较大。
这看起来像是个无厘头的循环论证,但事实就是如此。
玻尔兹曼指出,一切自发过程,总是从概率小的状态向概率大的状态变化,从有序向无序变化。
那么,我们又该如何理解“均值回归”呢?
从这个角度看,老赌徒们似乎又是对的:风水轮流转,连续的好天气后会下雨,一个人的运气会用尽,而触底之后会反弹,如塞翁失马般福祸轮转......
网络百科对“均值回归”这一概念的解释如下:
“起初是金融学的一个重要概念。均值回归是指股票价格、房产价格等社会现象、自然现象(气温、降水),无论高于或低于价值中枢(或均值)都会以很高的概率向价值中枢回归的趋势。”
赌徒谬误(小数法则),和均值回归,差别到底在哪里呢?
关键点,还在于样本量(以及时间的长短),以及对“均值在哪儿”的定义。
一个被高估的市场会回落,一个被低估的市场会反弹,然而,如凯恩斯所言:“市场保持非理性状态的时间可能比你保持不破产的时间更长。”
凯恩斯曾经利用保证金交易外汇,大赚,然后大亏。最后几乎一无所获。
这可是上个世纪最聪明的家伙之一,他当时对世界的预测准确得惊人,作为经济学家他也经常能“正确”判断货币走势。然而……
均值回归需要足够长的时间,就像大数定律需要足够多的随机事件的重复。并且均值回归还有“不均匀”和“不对称”的特点。
许多人和事件,无法实现足够多次重复,以及足够长的时间,从而导致无法享有“大数定律”与“均值回归”。
这就是所谓的没有“遍历性”。
某种意义上,长期主义的战略价值是:
1. 实现自己的遍历性;
2. 等对手因为丧失遍历性而被洗掉。
即使是在一个有期望值优势的游戏里,人们也可能赚不到钱。
凯利公式,本质上是通过控制下注比例来实现遍历性,并令回报最大。与之相反的行为,则是加杠杆。
后来,凯恩斯的投资转向于套利,以及重视价值的股票投资,回报大大好转。
看来,聪明人该犯的某些错误,很难因为非常聪明而不必犯。
六
与概率相关的基本计算惊人简单,但很容易让聪明人也犯晕。
例如概率的乘法定理:两个事件同时发生的概率,就是“第一个事件发生的概率”与“第一个事件发生时第二个事件发生的概率”的乘积。
为什么要说这么“绕”呢?
假如这两个事件是独立事件,二者发生互不影响,“第一个事件发生时第二个事件发生的概率”,即:给定第一个事件发生的条件下,第二个事件的条件概率,就是第二件事情独立发生的概率本身。
例如,扔两个骰子,得到两个“六”的概率是1/6×1/6=1/36。如此计算的前提是扔两个骰子是两个独立事件。
再看一道题,来自《牛津通识课:概率》:
假设在一所大学的研究生院中一半的学生是女生,并且1/5的学生学习工程学科。随机选择一个学生,请问,这个人是女工程师的概率是多大?
既然这个学生是女生的概率是1/2,这个学生学习工程的概率是1/5,那么是女工程师的概率不就该是(1/2×1/5=1/10)吗?
然而,这是错的。因为“是女生”和“学习工程学”并不是两个独立的事件。
这个时候,我们再回到乘法定理的定义,就知道正确的计算应该是:“这个学生是女生的概率”与“女生学习工程学的概率”的乘积。
因为传统上,“女生学习工程学的概率”,要小于“所有学生学习工程学的概率”,所以该学生是女工程师的概率要远小于1/10。
这只是个简单的中学数学题吗?这仅仅是语言游戏吗?
绝非如此。
我曾经看过一本难得的由院士写的科普书籍《机会的数学》,居然有评论者说该书只适合初中生以下的读者看。
而那本《牛津通识课:概率》的评分更是惨不忍睹。事实上,以该作者的深度和广度,以及跨越学科的洞见,进而还愿意并可以写成一本深入浅出的普及书,这类人我在国内几乎就没见过。
概率盲和科学盲一样可怕。(当然,概率是科学的一部分。)
我们不懂科学照旧可以刷手机炒房发财,然而不懂概率却可能让日子过得很糟糕。
现实中,许多重要的决策,唯一需要做的计算,就是这类概率乘法和加法。
然而,能够计算明白的人,非常罕见。
在两个因素并不独立的时候假设它们是独立的,是评估概率过程中最常犯的错误。
举个现实的例子吧:
有个朋友喜欢买房子投资。他信奉分散投资的道理,所以分别买了住宅和商铺,而且分散于所在城市的老区与新区。
然而,随着市场调整,他所在的三线城市房价全面回调,这时他才发现自己的所谓分散风险,就像泰坦尼克号那些没有封顶的水密隔舱。
又比如,一位地产大佬早早看出行业的势头不再,于是大力发展旅游地产,以分散住宅地产的风险。然而这“分散”因为旅游地产与住宅地产并不够相互独立而没能实现。
常识总是最重要的,可常识也需要加上概率的拐杖。
关于风险的常识更是如此。
七
弗雷德·马丁是一家投资公司的创始人,他的生存哲学是:避免可能导致致命后果的意外。
24岁时他曾是一艘驱逐舰上的中尉,当时他有一个习惯:每当他的军舰要转弯时,他都会走到舰桥上,用肉眼确认航道是畅通的。
我将类似于“军舰转弯”的这类情景,称为“决策点”。
许多时候,决策质量不够高,是因为决策覆盖率不够,有些决策点被忽略了。
这恰恰是区分决策者的专业程度所在。对于一名职业棋手而言,每一手棋都很重要,走出随手棋,看似无伤大雅,但经常是致命的。
对于巴菲特这类决策机器来说,所有关于钱的决策都需要全神贯注。所以早年他会因为老婆装修房子心痛不已,舍不得给女儿买电视,打投币电话都要去换个零钱。
这绝不只是因为吝啬,而是一种决策者的职业病。就像职业杀手晚上睡觉时的警觉。
决策的本质,是在不确定的情境下,为追求某种价值的实现,面向未来分配资源。
即使决策的过程是正确的,决策的结果却可能仍然很糟糕。
我们所面临的不确定性,大约是由三个要素构成的:
1. 现实世界的不确定性。虽然我们不确认造物主是在扔骰子,但目前看人类还只能用概率去逼近真相;
2. 人类认知体系的不确定性。理性的脆弱,感性的任性,是人类认知大厦的沙滩般的基础;
3. 人类作为决策主体的不确定性。
以上这些,又加上了数字化世界的种种混乱和失控。
斯多葛哲学在现代决策者人群中备受推崇,是因为其回答了在一个不确定的世界里“决策前、决策中、决策后”应该怎么办的难题。
然而,在我看来,许多对斯多葛哲学的理解是“错”的。
斯多葛哲学的前提,是承认世界的不确定性,承认个体的有限性,然后用一种控制二分法,来实现“现实的适应性”和“诗意的满足感”。
所谓“控制二分法”,是指:要区分你所能控制的东西和你所不能控制的东西。
你必须认知到外界的大多数事情是自己不能控制的,那么就应该接受 —— 不过分难过,也不必恐惧。
只从情绪控制和接纳自我等心理学的范畴看,依靠斯多葛哲学来实现这一点似乎说得过去。
可是,从决策的角度看,该如何区分哪些是能控制的,哪些是不能控制的呢?
这就有点儿像是说:你押硬币的正面会赚钱,押硬币的反面会亏钱。所以假如硬币正面朝上的可能性较大时,你要大胆下大注。
然而,我怎么知道硬币什么时候正面朝上的可能性较大呢?
几乎所有的智慧,都不会配一份现实操作指南。
多少人信奉巴菲特的“别人贪婪时我恐惧、别人恐惧时我贪婪”,结果,或是错过一牛再牛的大牛市,或是抄底抄在天花板。
八
我曾经构建过一个决策模型:
1. 每个决策构成一个闭环
该决策闭环的关键是“灰度认知+黑白决策”。
关于灰度认知。从概率角度看,当你面对一个60%胜率的(假设是一赔一的赔率)游戏时,你可以大胆选择去玩儿。60%介于0和100%之间,是一个灰度数值。
进而,连这个”60%胜率“的认知,在现实世界里也只是一种推测,一种信念。这是灰度认知的第二层含义。
关于黑白决策。当你玩儿上面那个60%胜率的游戏时,尽管这是个正确的决策,也有概率上的优势,但是你仍然有40%的可能性落在失败的空间里。
尽管如此,你也必须黑白分明地去完成这个决策,而不必也不能有任何犹豫和恐惧。
这就是为什么战场上战士必须无条件服从,以及基金经理和企业CEO非得有一刀砍向乱麻的决断力。
否则,会害死更多人。
即使是在一个决策的闭环里,一个人也会分裂成两个角色:一个负责“知”,一个负责“行”。
斯多葛的“控制二分法”,在这里该如何运用呢?
能控制的,到底是灰度认知,还是黑白决策?
灰度认知是我们能控制的东西,而黑白决策的结果则是我们不能控制的;
灰度认知只能是一种猜测,“真”的数值无法控制,而黑白决策必须坚定执行,所以是能控制的。
上述二者似乎都对,并且也非二元对立。
这时,维特根斯坦的洞见漂浮了出来:哲学家使用语言犹如一种游戏,他们已经不能表达实在的事物,只能靠词语之间的关联产生意义。
也许,这正是哲学很有用,又很没用的地方吧。
下面再看我的决策模型的第二部分。
2. 许多个决策构成了决策链条、决策网络,进而构成了一个体系
人的一生是由很多个决策穿起来的。
也许,最终决定命运的,只是其中最重要的几个。
然而,这几个最重要的决策,也是悬挂在由那些或大或小的许多个决策编织成的网络之上的。
就像蜘蛛不能仅编织能捕获猎物的那一小块儿网。
这许多个决策,通过基于大局观的重复,借助于时间的魔力,实现了连续性和稳定性,进而实现了复利;又或者,这许多个决策就像在某个赌场里不断地扔骰子而已。
那么,按照斯多葛的哲学,单个决策闭环,和整个决策体系,哪个是可以控制的?哪个又是不能控制的?
对于这个可以无穷尽讨论下去的话题,我想做个小结:
对于单个决策闭环而言,我们可以控制决策过程和质量,不必(也很难)控制决策结果;
对于整个决策体系而言,如果从人生的尺度看,我们可以控制旅途的意义,不必控制最终会到达何处。
这是我所理解的斯多葛多学。
九
综上所述,我们大致探讨了如下几个有趣的话题:
泰坦尼克号的16个独立的水密隔舱;
SpaceX龙飞船主控系统芯片组的6个独立但又能数据同步的内核;
概率中非常容易被弄混的“独立事件”概念;
“决策点”的独立性和连续性。
以上看似多元之话题的焦点,是我们当下时代最大的挑战之一:
这个世界如此充满“不确定性”,我们每个人必须全力以赴,避免遭受永久性的损失,永远不要像泰坦尼克那样沉没掉。
要做到这一点,我们要构建一个强健的系统,设计自己的“水密隔舱”,承受可能遭遇的各种风险,并能通过主动适应而升高生存的概率。
未来无法预测,我们既不能躺平,也不能无限制地安装更多救生艇,而是要千方百计在逆境中活下来。
活下来,活得久,就有机会实现“均值回归”,有机会让“大数定律”显形。
独立性给我们的另外一个重要启发是:你当下做的每一件事情都是独立的。
聚精会神打好当下的这个球,然后忘掉这个球。
几乎所有关于成功的故事,尤其是靠头脑和投资变得更富有的传奇,几乎都与独立思考有关。
你想要平均的收益,随大流是最好的做法之一。
如果你想要有超额的收益,你需要与众不同,特立独行,敢于和大多数人背道而驰,并且利用大多数人的非理性和羊群效应获利。
这一切的前提,是你的独立思考。
然而,何谓独立思考?
我们不止要独立于外部环境去思考,某种意义上,我们还需要独立于自己来思考。
人的自我的连续性,一直是个奇怪的谜团。
事件自动地、单向地、均匀地向前流动,也是一个谜团。
如此一来,人就很容易踩着西瓜皮向前。
设立决策点,能够让每个当下的“我”意识到:
“过去的你”是你的资产,也是你的“沉没成本”,现在的你必须与往事干杯,独立思考。
十
也许过去这几十年太美好了,以至于我们忽略了其神奇性。然而,即使是最好的游戏,哪怕胜率很高,赔率很好,也是有胜有负的。
因为害怕失败,害怕不确定性,而放弃自己的游戏权,其实就是放弃自己的概率权。
哪怕是糟糕的事情已经发生,也要挺住,稳住,为打好下一球做准备,别轻易出局。
进化只能在代际之间完成,财富往往要跨越周期才能实现,好运气也要靠遍历性之网来捕获。
无论如何,仍然要有希望,至少要对孩子充满希望——如此一来,你也依然有希望。
我们早已不是丛林时代的狩猎者或者被狩猎的对象。生活是一场游戏,暂时输一把也不会被老虎吃掉。
主管我们恐惧感的那一份大脑,是在漫长的远古时期形成的,我们的担忧被过度放大了。这种情绪又被数字化时代的传播再放大了十倍。
我们需要在一切悬而未决时保持平静,需要接受世间万物只是短暂“确定”的现实——这短暂已足以哺育我们。
我们该感慨的是自己何以如此幸运地存在于这个只有极小概率能够诞生生命的星球之上。
海明威这样写那位“可以被毁灭却不能被打败”的老人:
“除了那双眼睛,他浑身上下都很苍老。那双眼睛乐观而且永不言败,如大海一般蓝。”

世事无常,可只要我们心底的船不放弃,人生就永远不会沉没。
当我们遇见风险,只有面对,努力活下去,想办法重启,然后继续前行。
最后
此刻,我刚刚离开家,经历了漫长的跨洋飞行,和繁琐的出入境流程,在深圳的酒店隔离。窗外是东部华侨城的游乐园,大喇叭响个不停,游客稀少,整整一周雨下个不停。
这次回国出差,临走前要比往常做更多一些心理建设。孩子们照例有些失落,院子里的玫瑰和绣球花都还没来得及剪枝,山楂、葡萄和冬枣都等待采摘,朋友们则感慨我此际的出行。
和每个身处当下这个不确定世界的人一样,我也会对现实有所困惑。不管我多么积极向上,也会在深夜里问自己:“这是为什么呢?”
直到我看到金克木在《百年投影》的一段话:

我突然意识到,其实我可以同时是“诗人、凡人和智者”的:
在我的花园里,我就像一个过家家的孩子,岁月如童话般挂在郁郁葱葱的果树上。那时,也许我真的是一个做梦的诗人;
和每位为谋生为梦想而苦斗的人一样,我是个凡人,需要想办法为公司赚钱,操心生存的压力和未来的发展;
我还如此幸运地拥有“孤独大脑”,可以自由地写,还有你来看。也许我算不上智者,但却有智者沉思的乐趣。
这三个角色,像是一艘船的三个独立的水密隔舱。
如此一想,那种因为担心“凡人的失败”而伤害自己“做梦的花园”的忧虑,突然一下子消失了。
这三个“独立事件”,并非是狡兔三窟式的躲避或人格分裂,而是构成了我更丰富的、拥有冗余的生命系统:
1. 概率的乘法原理,以乘法的复利效应,为我构建了一个安全度极高的巢;
2. 我不会因为自己的“智者包袱”,而害怕去干“凡人”的蠢事。我不必为了“智者”的人设而逃避正确而艰难的事情,龟缩才是人生最大的风险;
3. 当我的某个系统感受到绝望时,另外两个系统会拥抱过来,用各自的希望来做数据同步,重启那个暂时熄火的发动机。
克尔凯郭尔曾经说过:不懂得绝望的人不会有希望。
而希望,才是永不沉没的秘密。
本文来自微信公众号:孤独大脑(ID:lonelybrain),作者:老喻
