相变
物理系统中发生的相变最直观,水结成冰或沸腾成蒸汽。在一定的温度或压力下,系统发生行为的突然变化,从一种相转变为另一种相。转变出现了之前相中没有的新特性,例如冰的晶体结构或蒸汽的气态特性。
相变应该是自然界的基本特征之一,例如科学家发现即使在绝对零度,量子涨落也可引发量子相变。相变普遍存在于从原子到星系等各种系统中,而且不限于物理系统,化学、社会、经济、生物进化、脑科学和信息系统等等领域也普遍存在。股市的突然崩盘、抗议活动的爆发就可以被看作是社会系统中的相变。
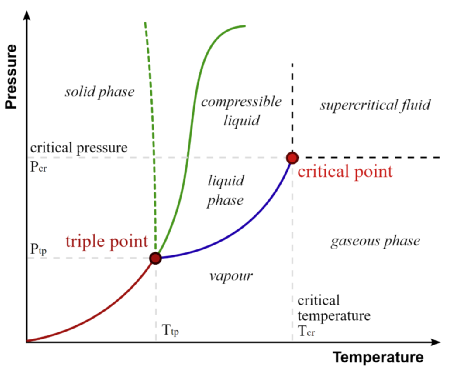
那“相”是什么呢?以物理系统为例,仔细体会,"相"其实是空间密度函数,而且是随时间变化的空间密度函数,ρ ( Space , T )。空间密度函数的突变,就是相变。如果我们把物体里面的原子密度函数写作 ρ,然后用一组基函数 ϕi 把 ρ 展开 ρ=Σηiϕi,即把密度函数展开成了空间里的一个矢量 η。也就是基函数 ϕi 张成的空间中,ρ 可以表示成向量η 。这样“相”也就可以表征成 η的函数:“相”= F (η)。这样相变就被刻画成了数学形式。笔者一直试图抑制使用数学公式的冲动,但这里表述起来很方便,且可以为读者学习朗道相变理论开个头,看看朗道如何将复杂物理现象建模成数学问题。
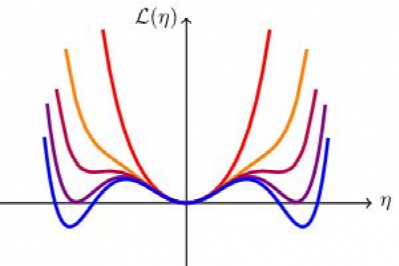
相变也可以被视为一个临界点(Critical Point),系统的行为在此临界点处会发生突变。在这个临界点上,温度或压力的微小变化可以导致系统性质的巨大改变。这是因为系统处于两个相之间的边界上,小的扰动可以推动它落入其中一个相或另一个相。相变可能导致出乎意料的涌现(emergent) 现象。理解相变可以帮助我们更好地理解和预测复杂系统中的这些突然变化,以便更好的理解和掌握涌现现象。
复杂系统涌现
1977 年诺贝尔物理学奖得主菲利普 · 安德森在 Science 上发表了他的传世之作《More Is Different》,书中安德森认为复杂系统就是不能简单地归纳为其各部分之和的系统。因为这些系统的行为不能通过研究其个体组成部分来预测。他运用物理学、生物学和社会学等领域的例子说明了这一点,强调了复杂系统的涌现现象不能简单地通过了解其个体部分的属性来解释。
复杂系统表现出的涌现现象,并不在单个组成部分中存在。涌现是由系统组件之间的相互作用和关系产生的新属性,仅仅通过研究单个组件是不能解释的。牛顿力学导致的精确极致的还原主义不是有效地理解复杂系统的方法。在某些情况下,研究系统的组成部分可能反而会导致有关整个系统的信息丧失。这是因为涌现经常源于系统组件之间的相互作用,而单独研究组件可能会掩盖这些相互作用。
铁磁材料的磁性质,低温下某些材料的超导性,都是来自材料中原子与电子的集体行为,生物系统蚁群或鸟群的行为,语言、文化和政治制度等社会现象,都不能仅仅通过理解个体的特性来解释,而是需要了解他们的集体行为和互动。
对称性破缺
相变往往伴随着新对称性或对称性破缺的出现,这可以揭示系统涌现行为的深层次原理。这里有个非常关键的专业概念:对称性破缺。专业的说法,“对称性破缺是一个跨物理学、生物学、社会学与系统论等学科的概念,狭义简单理解为对称元素的丧失;也可理解为原来具有较高对称性的系统,出现不对称因素,其对称程度自发降低的现象。”
想象一支铅笔竖立在桌子上。铅笔是对称的——从所有平视角度看起来都一样。但是,如果你敲打桌子,铅笔会倒在一个方向上。这就破坏了铅笔位置的对称性,从不同的角度看起来它就不同了。
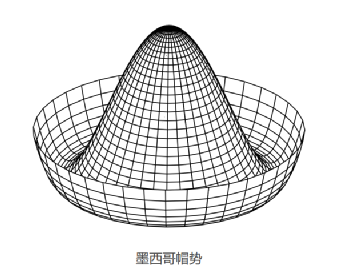
在物理学中,对称性破缺也是一个类似的过程。一个系统可能具有对称性,但如果经历了变化或干扰,它可能会打破对称性,采取一个新的、不同的配置。“墨西哥帽”是对称性破缺的常见教科书案例。
对称性破缺的现象同样也会出现在语言学习和大型语言模型中。在语言学习中,当学习者遇到新的语言结构或规则时,对称性破缺现象可能就会发生。例如,如果一个以英语为母语的人开始学习汉语,他们最初可能会假设中文的句子结构与英语类似。然而,他们很快就会发现中文的句子结构是不同的,这一认识打破了他们关于语言的先前对称性的假设。
大模型语言结晶
类似地,在像 GPT-3/4 这样的大型语言模型中,当模型在大规模数据集上进行训练并遇到新的、以前未见过的语言模式时,对称性破缺现象也会发生。随着模型遇到这些模式,它对语言的理解可能会发生变化和适应,导致一种新的配置,打破了其语言空间刚刚建立的对称性。
没有预训练的Transformer是一张各向对称的白纸,也就是其语言空间的密度函数ρ是均匀的。这个语言空间的密度函数决定了系统的信息熵,如果我们仍然把 ρ 表示成向量 η,则信息熵可以表示为F(η).随着语料不断被 emdedding 同时基于注意力机制 transform到这个语言空间,空间的密度ρ/η发生改变,信息熵 F(η)随着改变,引发语言空间对称性破缺与重建。这个过程可能会在局部区域不同尺度下持续的进行。一旦触及临界点,对称性破缺引发相变,大模型就会在某些领域、不同长度上下文表现出各种神奇的涌现能力。
这里笔者借助对称性破缺,解释了 GPT 内部语言概率空间的微扰,导致其语言空间对称性的破缺,形成秩序,结成语言晶体。即语言概率空间的密度函数,向着更有序的方向相变。然而破缺可以随机到一个相或另一个相,演化方向是很难预知的。这就凸显了训练数据集的重要性,新引入的数据集会增加系统的对称性,还是降低?即系统的信息熵增加还是降低?这些改变是整体还是局部进行?从目前GPT4 与GPT3的能力对比看,出现了整体大幅提升而局部降低的现象,或许是微扰导致局部特定尺度的破缺向更无序方向相变使然。
重整化群
对称性普遍存在于各个尺度下的系统中,有对称性的存在,就必然存在对称性的破缺。重整化群(Renormalization Group) 是研究不同尺度下对称性破缺与重建过程的核心数学手段。借助重整化群这一研究复杂物理系统行为的框架,人们可以在不同尺度上分析系统,并理解随着观察尺度的变化,系统的特性如何变化。通过这种方式,RG提供了一种研究微观细节如何产生较大尺度新涌现特性的方法。

