** PART.0 长相离谱的张量转置**
注:此转置操作与 t-product 积相对应,在其他类型张量运算中的转置操作可能有不同的定义方式,请注意区分。

简单描述一下:
我们把三维张量每一个frontal slices(面向我们的切片),进行转置,然后将序号2到n的切片顺序完全反过来,图片描述如下:
假如以下为原始张量:
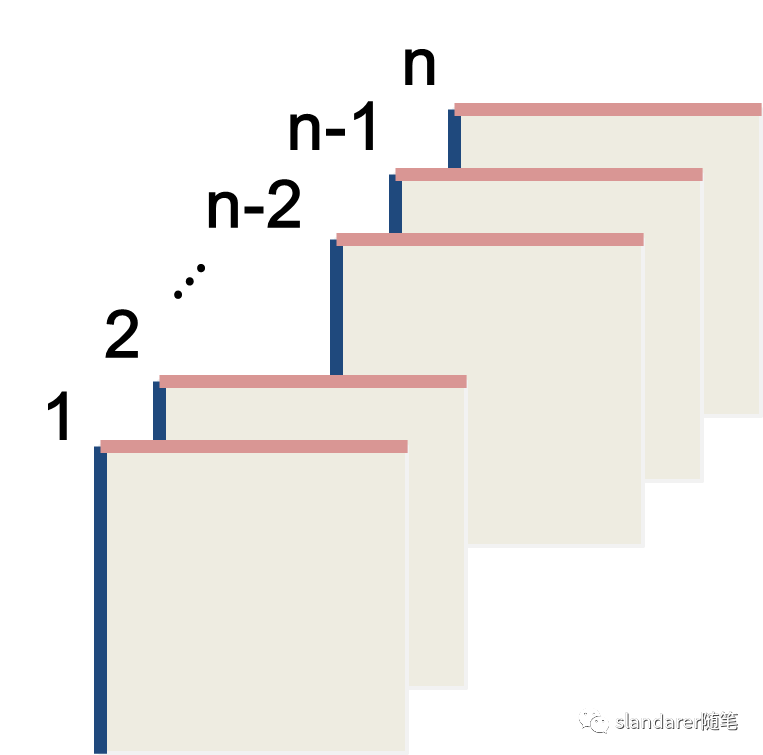
转置完成后:
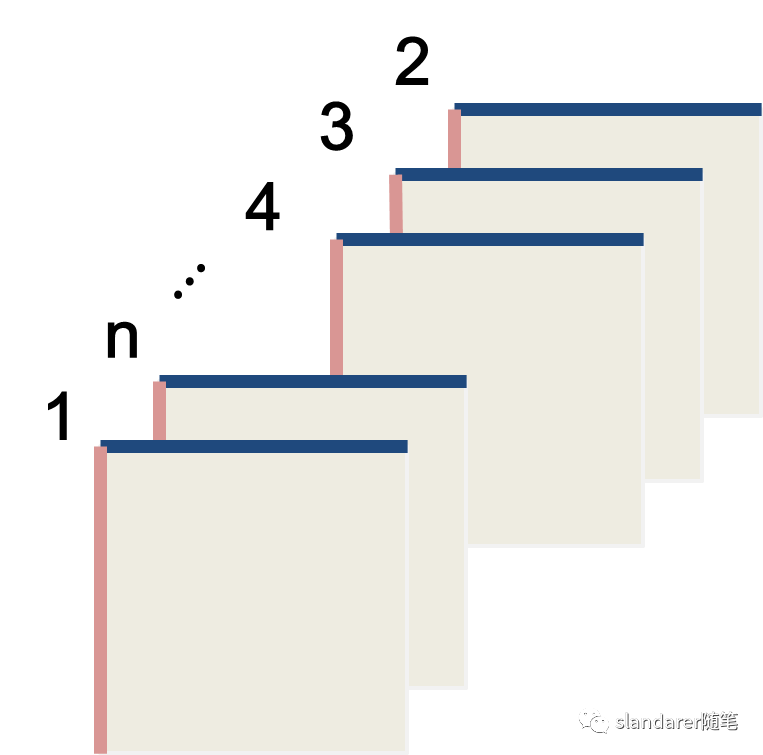
那么。。。为什么会有如此的操作呢,其实这都是为了之后的张量inside product做准备(不叫做内积是因为有某些性质不符合内积的定义),和向量内积很像,张量内积也需要其中某个张量转置之后和另一个张量做 t-product 积,既然是做 t-product 积,就要迁就于 t-product 积的某些性质。
这里再重提一下 t-product 积的定义:

** PART.1 转置的特殊性质**
首先说明一下 squeeze 操作及 twist, 简单一张图就可以描述:
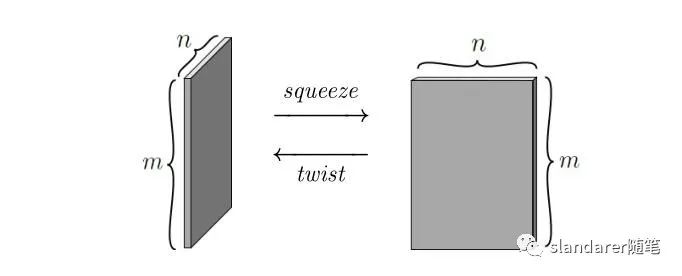

这都可以相等。。very amazing 啊 ,光证明出来咋能不验证呢?
** PART.2 MATLAB实现**
我们编写如下 MATLAB 程序(引用的子函数放到最后):
X=zeros([2,1,3]);
X(:,:,1)=[1;2];
X(:,:,2)=[3;4];
X(:,:,3)=[5;6];
c=zeros([1,1,3]);
c(:)=[1,2,3];
squeeze(t_prod(X,c))
squeeze(X)*bcirc(t_T(c))
ans =
20 20 14
26 26 20
ans =
20 20 14
26 26 20
左右两边运行结果一致,非常完美,另外各个子函数如下:
t-product
function C=t_prod(A,B)
% @author:slandarer
% 用于进行张量t-product积
% A*B=fold(bcirc(A)·unfold(B))
% 获取张量大小
[l,p,n]=size(A);dimA=[l,p,n];
[p,m,n]=size(B);dimB=[p,m,n];
dimC=[l,m,n];
if dimA(2)~=dimB(1) || dimA(3)~=dimB(3)
error('Inner tensor dimensions must agree.');
end
% 对A,B进行unfold展开操作
ufold_A=reshape(permute(A,[2,1,3]),dimA(2),[])';
ufold_B=reshape(permute(B,[2,1,3]),dimB(2),[])';
% 对A构建循环矩阵
bcirc_A=zeros([l*n,p*n]);
for i=1:n
bcirc_A(:,(1:p)+(i-1)*p)=circshift(ufold_A,l*(i-1),1);
end
% bcirc(A)·unfold(B)
AB=bcirc_A*ufold_B;
% 还原张量维度
C=ipermute(reshape(AB',dimC([2,1,3])),[2,1,3]);
end
张量转置
function AT=t_T(A)
% @author:slandarer
% 应对与张量t-product积的转置
[l,m,n]=size(A);
AT=zeros([m,l,n]);
% fronral slices转置
for i=1:size(A,3)
AT(:,:,i)=A(:,:,i)';
end
% 径向重排序
if size(A,3) >1
AT(:,:,1:end)=AT(:,:,[1,end:-1:2]);
end
end
squeeze
function squeezeX=squeeze(X)
% @author:slandarer
% lateral slice 翻转
if size(X,2)==1
squeezeX=permute(X,[1,3,2]);
else
error('MyComponent:incorrectType',...
'Error input: nInput must be a lateral slice.')
end
end
bcirc
function bcircA=bcirc(A)
% @author:slandarer
% 用于张量展开为循环矩阵
% 获取张量大小
[l,p,n]=size(A);dimA=[l,p,n];
% 对A进行unfold展开操作
ufold_A=reshape(permute(A,[2,1,3]),dimA(2),[])';
% 对A构建循环矩阵
bcircA=zeros([l*n,p*n]);
for i=1:n
bcircA(:,(1:p)+(i-1)*p)=circshift(ufold_A,l*(i-1),1);
end
end
