数值型数据的表示
在计算机中,无论是何种形式的数据均采用数字化形式表示,即用“0”、“1”两个基本符号构成的编码表示,以便采用数字电路实现其存储与处理。
- 本节主要内容
- 数制
- 数的机器数
- 定点与浮点格式
数制
二进制阅读、书写不方便,引入八进制、十六进制。它们与十进制之间以及相互之间如何转换?
各种数制
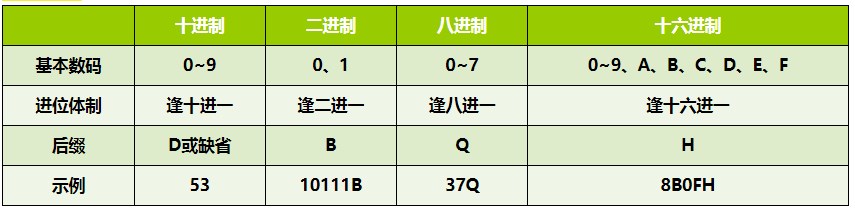
数制之间的转换
- N进制 ➡ 十进制 “按权展开再相加”
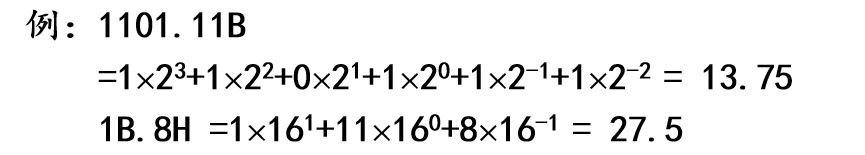
- 十进制 ➡ N进制 整数部分:除N直到商为0,倒取余 小数部分:乘N直到精度满足要求,正取整 例:28.628 = 11100.101B
- 十进制 ➡ N进制
十进制转换二进制,常用凑数法。

- 二进制 ➡ 十六进制
以小数点为中心,向左右两边4位一组,不够4位的左边前补0,右边后补0,然后把每4位写出对应的十六进制数。

- 十六进制 ➡ 二进制
将每一个十六进制数码写成对应的4位二进制码,前后的无效0去掉。

二进制与八进制间的互换与十六进制间的互换类似。
机器数
真值
正号(+)、负号(-)加二进制或者十进制的数值表示数据大小的形式在计算机原理中称为真值。 如:+1011101B,或 -123.45
其中:“+”号经常省略。
机器数
数据在计算机中存储或处理的数据形式称为机器数。
正、负号也要用0、1表示。
机器数分有无符号数和有符号数。
无符号数
整个机器字长的二进制位均为数值位,没有符号位。相当于数的绝对值。
例如:10000011B表示十进制无符号数的131。
字长为n位的无符号数的表示范围为0~2(n)-1。
若字长为8位,则表示无符号数的范围为0~255。
有符号数
约定:机器字的最高位为符号位,其余位为数值部分。一般“0”表示正数,“1”表示负数。
例如:真值为-1011101B的机器数可以表示为:
11011101。
符号位和数值位如何联合表示一个数?计算机中有多种编码形式,以适应不同的应用场合的需要。常用的编码形式有:
- 原码
- 反码
- 补码
- 移码
一、原码
- 定义:
最高位为符号位,0表示正,1表示负,的数值部分为真值绝对值。
即:除去符号用0或1表示外,其余部分与真值(二进制)相同。
例如,8位机中,x=+1001101时,x=01001101
x=-1001101时,x=11001101
再如,5位机中,x=+0.1001时, x=0.1001
x=-0.1001时, x=1.1001
- 原码定义的数学表达式---用于一些数学推理
若真值x为纯整数数,n位机中:
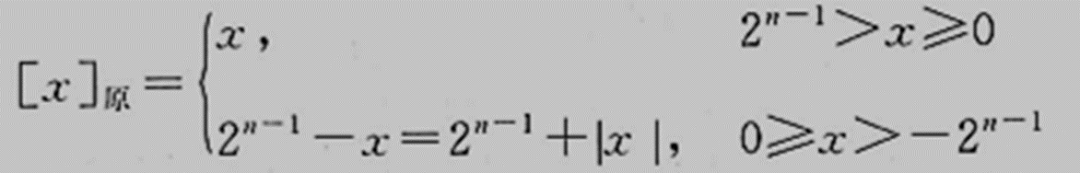
若真值x为纯小数,n位机中:
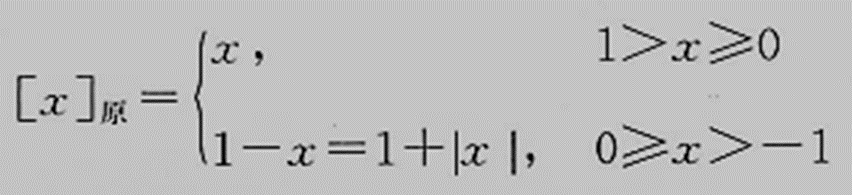
根据原码的定义,0的原码有两种不同的形式:
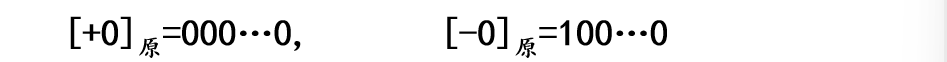
原码表示的数据范围
纯整数n位机中:
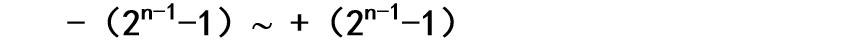
纯小数n位机中:
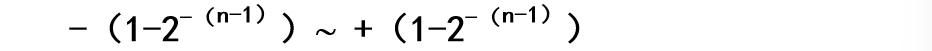
优点:直观易懂,与真值之间转换简单;
实现乘、除法运算规则简单。
缺点:实现加、减运算的规则较复杂,电路实现困难。
二、反码
-
定义
正数的反码和原码相同;
负数的反码是将原码中符号位不变,数值部分中的各位变反。
例如:
8位纯整数机中,
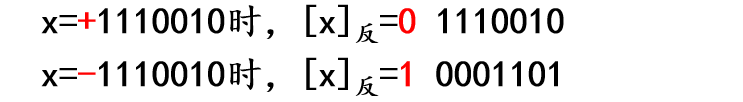
8位纯小数机中,
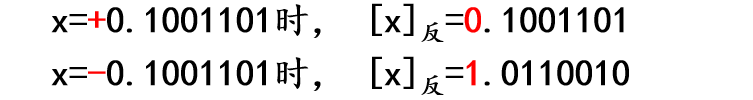
-
反码特点
-
0的反码也有两种不同的形式:
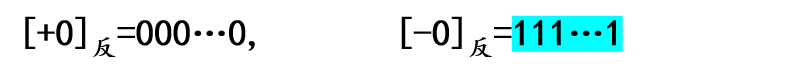
-
表示的数据范围与原码一样:
纯整数n位机中:
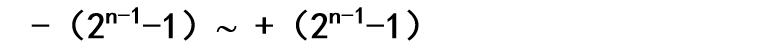
纯小数n位机中:
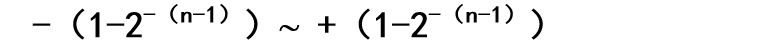
三、补码
是否能将减法运算化为加法?
(1)模和补数
- 以钟表为例,假设当前时针指向8点,若要将时针拨到6点,有两种方法:
逆时针拨2小时,或顺时针拨10小时。
前者代表8-2=6,后者可以认为是8+10=6(mod 12)。
在模为12时,-2和+10等价。称-2的补数是10。
- 启发:减法运算可以转换为加该数的补数。
补码定义
有符号数x的补码定义为:

对于n位纯整数机,其模为2(n) ,数x的补码为:
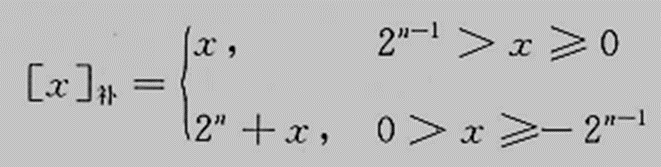
对于n位纯小数机,其模为2 ,数x的补码为:
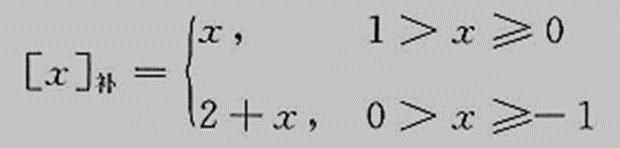
按照定义求补码
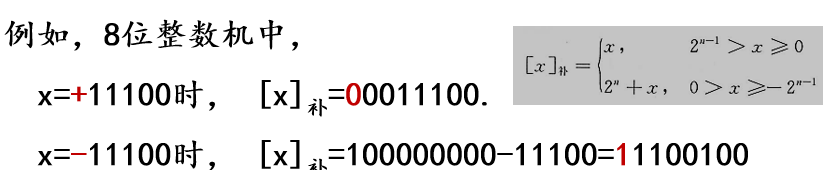
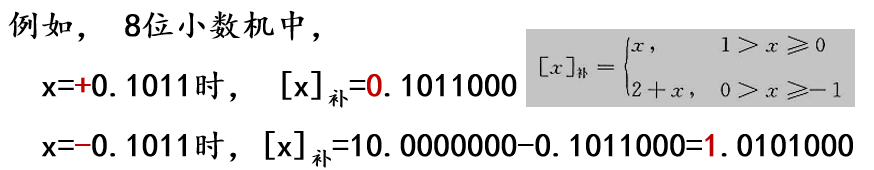
补码****表示的数据范围
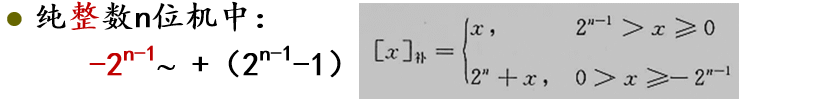
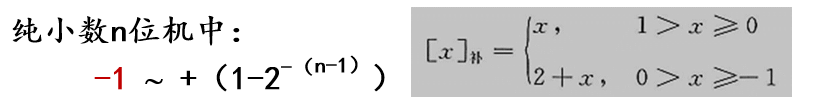
注意:
补码表示的数据范围比原码在负数方向多一个值。
补码中,100...0中的最高位1既表示符号,又是数值位。
如,8位整数机,10000000是-128的补码;
8位小数机,1.0000000是-1的补码。
根据补码的定义,0的补码表示只有形式:000…0
定点和浮点格式
定点格式表示的数据范围
有符号数的编码不同,所表示的数据范围不同。


四、移码
移码主要用于表示浮点数的阶码。由于阶码是整数,这里只讨论x是整数时的移码。


注意 : 移码符号位****的表示规律与原码、反码、补码的相反。
移码特点
如果将移码看作无符号数,其大小直观地反映了真值的大小。移码全为0时,所对应的真值最小,全为1时,所对应的真值最大。因此,浮点数的指数(阶码)常用移码表示。这样比较两个浮点数大小时,阶码编码大数就大。
四种编码小结
各有所长,分别使用在不同的场合。补码表示时加减运算方便,目前机器中广泛采用补码存储和运算。有些机器做加减运算时采用补码,做乘除运算时采用原码。移码主要用于表示浮点数的阶码。
同一个二进制码,所表示的含义不同,相对应的实际值不同。下表给出8位二进制码00000000~11111111含义不同时,与其实际值之间的相应关系。
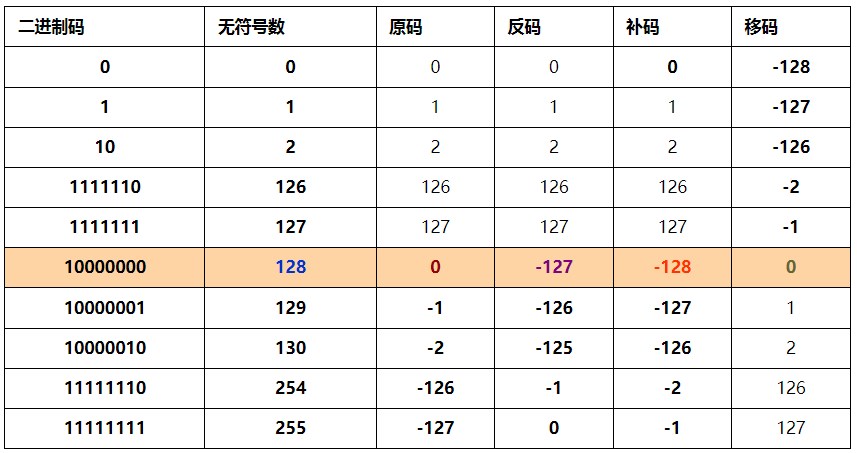
在计算机中,小数点的问题如何解决?
计算机中,没有专门设置电路来表示数据的小数点,而是采用不同的数据格式约定小数点的位置。
常用的数据格式:
- 定点格式
- 浮点格式
定点格式
-
约定机器中小数点在数据编码中的位置固定不变。
-
由于已约定,机器中不再用“.”记号表示。
-
任意n位定点数x,在计算机中的格式为:
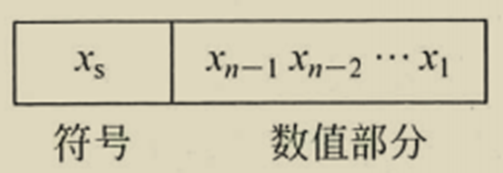
-
理论上讲,小数点可以固定在任何位置。但计算机设计时通常将数据设定为纯小数和纯整数两种。
定点格式表示的数据范围
有符号数的编码不同,所表示的数据范围不同。


- 将其转化为定点机所能处理范围内的数据,得到的运算结果再根据比例因子还原成实际值。
- 定点格式所能处理的数据范围十分有限。如果同时有绝对值非常大或绝对值非常小的数,用同样的比例因子进行处理,很难兼顾数值范围和运算精度的要求,为此引入浮点数表示。
浮点格式—浮点数
- 浮点数:小数点在数据中的位置可以浮动。
- 任意一个R进制数N,其浮点数可以写成:
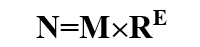
其中:
- M尾数:表明数据有效位数,决定了数据的精度。
- E阶码:一个整数,指明小数点的位置。决定数据的大小。
- R基数:计算机中一般规定为2、8或16。
例如,二进制数101.00101的浮点数形式可以写成:
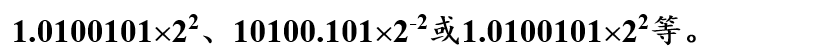
- 阶码的取值不同,小数点的位置在尾数中进行浮动。
浮点格式— 一般格式
- 浮点数的一般格式为:
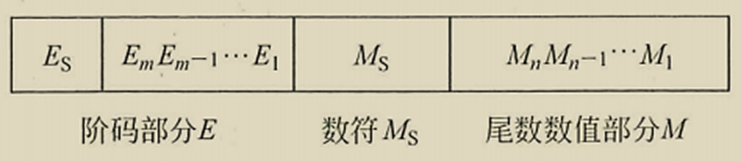
基数约定为2,阶码E和尾数M是有符号数。
- 浮点数的具体格式有很多种形式:
- 尾数和阶码可采用不同的机器码
- 数符的位置也可放在首位
- 多数尾数是纯小数,采用原码或补码表示。IEEE754浮点格式尾数采用1.M形式。
- 阶码为纯整数,可以采用补码或移码表示。
浮点格式—表示的数据范围
- 浮点格式表示的数据范围主要由阶码的位数决定,精度主要由尾数的位数决定。
- 阶码和尾数采用的机器码不同,其所能够表示的数据范围不同。
- 例如:32位浮点格式,阶码8位(含阶符1位)移码表示;尾数24位(含数符1位)补码表示。

浮点格式—表示的数据范围
32位浮点格式,阶码8位(阶符1位)移码表示;尾数24位(含数符1位)补码表示。其能表示的数据范围:

显然,浮点格式表示的数据范围比定点格式要大很多
浮点格式—机器零
机器零的规定:
- 浮点数的尾数值为零时;
- 阶码小于机器所能表示的最小值时;
浮点格式—规格化
-
同一数的浮点表示形式是不唯一的。
例如:二进制数101.00101的浮点数可以写成:
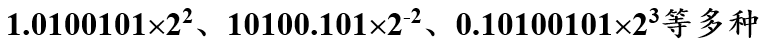
-
规格化的概念
-
为了充分利用尾数有限的位数,提高运算的精度,存储数据中尽可能多是有效数字。
-
规定:浮点数尾数值不为0时,其最高数值位应是有效位,即尾数的绝对值应大于或等于0.5。这种形式的浮点数称为规格化浮点数。

-
规格化浮点数的形式
-
编码 0.1001000的浮点数是规格化;
-
编码 1.0000100的浮点数也是规格化;
-
编码0.1001000的浮点数是规格化;
-
编码1.1000100的浮点数也是规格化;
-
尾数采用原码表示时,尾数最高数值为1。如:8位尾数,
-
尾数采用补码表示时,尾数符号和最高数值位一般应为01或10的形式。如:8位尾数,
-
注意一种特例:当尾数补码表示,尾数值是-0.5时,其对应的补码为1.1000000,不是01或10的形式,也满足规格化要求。
-
规格化处理
方法:对尾数进行移位,直到满足上述规格化要求。尾数每左移一位,阶码减1;尾数右移一位,阶码加1。

- 若尾数原码表示,
- N的浮点格式为0011 10010100
- 规格化后N的浮点格式:0001 11010000
- 若尾数补码表示,
- N的浮点格式为0011 11101100
- 规格化后N的浮点格式为:0001 10110000
浮点格式—IEEE754浮点格式
-
为了便于软件的移植,1985年IEEE(Institute of Electrical and Electronics Engineers)制定了IEEE754浮点格式标准。
-
IEEE754浮点格式:

-
阶码E移码表示 (-3+127) = 124 = 0111 1100
-
尾数原码表示,且尾数整数部分为1,缺省存储
-
真值为:


- IEEE754规定了三种浮点数的格式:单精度、双精度和扩展精度。
- C语言中float和double型数据为IEEE754存储格式
单精度浮点数格式:

双精度浮点数格式:

说明:阶码为全0和全1规定表示一些特殊的数值:
- E为0,且M为0时,表示机器0;
- E为全1,且M为0时,表示±∞;
- 若E为全0,而M为非0,IEEE754认为是非规格化数;
- 若E为全1,而M为非0,IEEE754认为是NaN(Not a Number非数值)数据。
- IEEE754规格化普通数:M非0,阶码E的值在1
254(或12046)之间,对应的实际指数值为-126+127(或-1022+1023)。
十进制数串的表示
十进制数有两种存储和处理形式:字符串和压缩的十进制数串。
1.字符串形式
- 把十进制数串当作一个字符串,每一个十进制数位及其正、负符号都用相应的ASCII码表示,各占一个字节,连续存放。
- 例如,数-352字符串存储形式:

*造成存储空间的浪费,数据处理不便,一般用于非数值计算的应用领域中。
2.压缩的十进制数串形式
-
一个字节存放两位十进制数的BCD码,常采用8421码。
-
符号也用4位二进制编码表示,存放在最低数值位之后。
例如,-2648的的压缩十进制数串表示为:

节省存储空间,便于算术运算,广泛采用。
【知识拓展】 BCD码
用4位二进制数表示一位十进制数的编码称为BCD码(Binary Code Decimal)。
从4位二进制的16个编码中选取10个编码表示十进制的10个数码,方法可以有很多种。常用的有8421码、2421码、余3码、Gray(格雷)码等。